¶ Ausgewählte Probleme
¶ Suchealgorithmen: linear und binär
Finden eines Elements in einer Datenstruktur.
Problemgröße: Länge der Liste
Kostenmaß: Vergleiche
¶ Linear
- Starte am ersten Element
- Vergleiche mit dem Suchelement
a) wenn gefunden, dann fertig
b) sonst gehe zum nächsten Element: Wiederhole Schritt 2.
Komplexitätsklasse:
- BestCase: O(1)
- WorstCase: O(n)
¶ Binär
Vorbedingung: Liste ist sortiert.
- Starte mit mittlerem Element der Liste (wenn n gerade, nimm das Element links von der Mitte)
- Vergleiche mit dem Suchelement
a) wenn gefunden, dann fertig
b) wenn Wert > Suchelement: wiederhole 2. mit mittlerem Element der linken Teilliste, sonst mit der rechten Teilliste
Komplexitätsklasse:
- BestCase: O(1)
- WorstCase: O(log(n))
¶ Beispiel
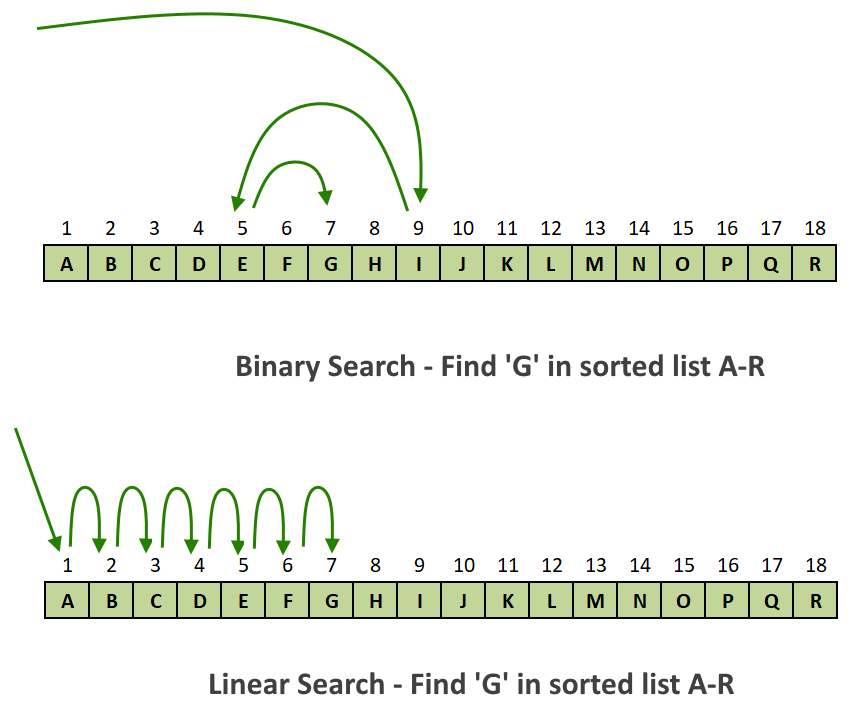
¶ In Python (für Interessierte)
def lineare_suche(liste, ziel):
for index in range(len(liste)):
wert = liste[index]
if wert == ziel:
return index
return -1
def binaere_suche(liste, ziel):
links = 0
rechts = len(liste) - 1
while links <= rechts:
mitte = (links + rechts) // 2
if liste[mitte] == ziel:
return mitte
elif liste[mitte] < ziel:
links = mitte + 1
else:
rechts = mitte - 1
return -1
# Testaufrufe
daten = [1, 3, 5, 7, 9, 11]
print("Lineare Suche:", lineare_suche(daten, 7)) # Ausgabe: 3
print("Binäre Suche:", binaere_suche(daten, 7)) # Ausgabe: 3
print("Lineare Suche (nicht gefunden):", lineare_suche(daten, 4)) # Ausgabe: -1
print("Binäre Suche (nicht gefunden):", binaere_suche(daten, 4)) # Ausgabe: -1
¶ Rucksackproblem (knapsack problem)
Finde die wertvollste Kombination von Gegenständen für einen Rucksack mit einer begrenzten Kapazität (z. B. Gewichtslimit).
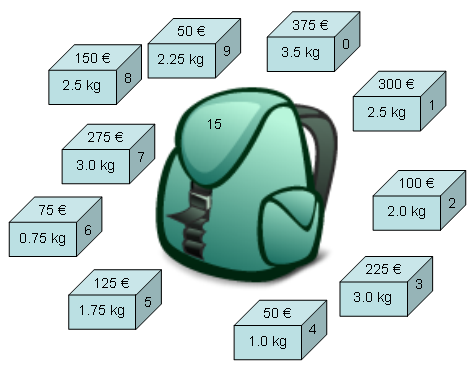
Problemgröße: Anzahl der Gegenstände
Kostenmaß: Berechnung Gewicht/Kosten für eine Kombination
¶ Bruteforce
Komplexitätsklasse: O(2n)
Kann als Tabelle dargestellt werden. 0 = nicht einpacken; 1 = einpacken
| Gegenstand 3 | Gegenstand 2 | Gegenstand 1 | Gewicht | Wert |
|---|---|---|---|---|
| 0 | 0 | 0 | ... | ... |
| 0 | 0 | 1 | ... | ... |
| 0 | 1 | 0 | ... | ... |
| 0 | 1 | 1 | ... | ... |
| 1 | 0 | 0 | ... | ... |
| 1 | 0 | 1 | ... | ... |
| 1 | 1 | 0 | ... | ... |
| 1 | 1 | 1 | ... | ... |
- Berechne für alle Kombinationsmöglichkeiten das Gewicht
- Wenn Gewicht unten dem Limit des Rucksacks: berechne den Gesamtwert
- Wähle den maximalen Wert
¶ Näherungslösung (Heuristik)
Eine Nährungslösung bzw. Heuristik ist eine vereinfachte, oft schnelle, aber nicht unbedingt perfekte Methode, um ein Problem zu lösen.
¶ Greedy-Lösung
Für das Rucksackproblem kann eine Näherungslösung durch einen Greedy-Algorithmus bestimmt werden.
Ein Greedy-Algorithmus (auf Deutsch häufig "gieriger Algorithmus") ist ein Algorithmus-Paradigma, bei dem man Schritt für Schritt die jeweils lokal beste Entscheidung trifft. Dieses Verfahren ist meist effizient, führt aber nicht unbedingt zur idealen Lösung.
Greedy-Lösung für das Rucksackproblem
- Berechne für jeden Gegenstand Wert/Gewicht (Quotient)
- Wiederhole bis Rucksack voll: Packe den nächstwertvollsten Gegenstand ein
Der Algorithmus ist effiziert, findet aber nicht sicher die beste Lösung.
¶ n-Damen Problem
Platziere n Damen auf einem n×n-Schachbrett so, dass keine zwei Damen einander schlagen können.
Problemgröße: Anzahl der Damen (= Höhe = Breite des Feldes)
Beispiel für n = 4

¶ Bruteforce
Erstellung und Überprüfung aller möglichen Positionen
Komplexitätsklasse: O(n!), da für erste Dame n*n Möglichkeiten, für die zweite n2-1, n2-2, usw.
¶ Verbesserte Ansätze (immernoch Bruteforce)
- Nur eine Dame pro Zeile: O(nn)
- Backtracking: Lösung wird Schritt für Schritt aufgebaut. Bei Bedarf wird zurückgegangen („backtracken“), wenn sich ein gewählter Teilschritt als ungeeignet erweist. Elegantes Vorgehen, dass aber nicht die Komplexität reduziert.
Simulation: https://www.mathematik.ch/spiele/N_Damenproblem/
¶ Handlungsreisender
Ein Handlungsreisender soll eine Anzahl von Städten besuchen. Er möchte:
- jede Stadt genau einmal besuchen und
- am Ende zum Ausgangspunkt zurückkehren,
- die Gesamtstrecke dabei möglichst kurz halten.
Problemgröße: Anzahl der Städte

¶ Bruteforce
Kostenmaß: Berechnung der Distanz für eine Kominationen
Komplexitätsklasse: O(n!), da n! Kominationen möglich
¶ Greedy-Lösung
Bis alle Städt besucht wurden: Besuche als nächstes die Stadt, die zuvor noch nicht besucht wurde und am nächsten an der aktuellen Stadt liegt.
¶ Primfaktorzerlegung
Maybe later