¶ Effizienz
Zwei Algorithmen heißen äquivalent, wenn sie bei gleichen Ausgangszuständen jeweils gleiche Endzustände erzeugen.
Von zwei äquivalenten Algorithmen heißt derjenige effizienter, der mit weniger Ressourcen (d.h. Rechenzeit oder Speicherplatz) auskommt.
Die Effizienz von Algorithmen spielt bei der Bewertung eine wichtige Rolle. Sie lässt sich experimentell und theoretisch bestimmen.
| Aspekt | Experimentelle Analyse | Theoretische Analyse (O-Notation) |
|---|---|---|
| Ziel | Messung der tatsächlichen Laufzeit oder Ressourcennutzung | Abschätzung des Wachstumsverhaltens eines Algorithmus |
| Abhängigkeit von Hardware | Abhängig von Hardware, Betriebssystem und Implementierung | Unabhängig von Hardware und Implementierung |
| Aussagekraft | Liefert exakte Werte für bestimmte Eingaben | Zeigt, wie sich die Laufzeit bei großen Eingaben verändert |
| Konstanten und Details | Konstanten und reale Effekte werden berücksichtigt | Konstanten und niedrige Terme werden ignoriert |
| Vergleichbarkeit | Vergleich nur unter gleichen Testbedingungen sinnvoll | Einfacher Vergleich verschiedener Algorithmen möglich |
| Genauigkeit | Genau, aber nur für die getesteten Fälle | Abstrakt, nicht exakt |
| Einsatzgebiet | Praxisnahe Leistungsbewertung auf realen Systemen | Analyse des asymptotischen Verhaltens (z. B. bei großen ( n )) |
¶ Theoretische Analyse
Die theoretische Analyse teilt Algorithmen in Komplexitätsklassen ein.

¶ Beispiele
| Komplexitätsklasse | Name | Beispiel |
|---|---|---|
| O(1) | konstant | |
| O(log n) | logarithmisch | |
| O(n) | linear | |
| O(n log n) | linear logarithmisch | |
| O(n2) | quadratisch | |
| O(2n) | exponentiell | |
| O(n!) | Fakultät |
¶ Durchführung Analyse
Merke: Wir suchen keine genaue Berechnung, sondern nur eine Annährung für große Problemgrößen n.
- Festlegung der Problemgröße n: Am Beispiel von Sortierverfahren ist n die Länge der Liste.
- Festlegung des Kostenmaßes, also der Operationen, die betrachtet werden sollen und maßgeblich für den Algorithmus sind. Beispiel für Sortierverfahren: Vergleich
- Berechnung, wie häufig die Operationen des Kostenmaßes ausgeführt werden.
- Streichung aller konstanten Termen. Nur der am stärksten wachsende Term bleibt übrig. (Bestimmung des Grenzwertes)
¶ Cases
Häufig ist die Laufzeit nicht nur von der Problemgröße abhängig.
- best case (bester Fall): der Fall, in dem bei der Ausführung des Algorithmus die wenigsten Kosten anfallen
- worst case (schlechtester Fall): der Fall, in dem bei der Ausführung des Algorithmus die meisten Kosten anfallen
- average case (durchschnittlicher Fall): eine Mittelung der Kosten über alle Fälle
Der durchschnittliche Fall ist idR. in der Praxis der wichtigste Fall. Er ist allerdings schwer zu ermitteln, so dass das wir uns erstmal auf den worst case fokussieren.
¶ Beispiele
¶ Einfacher Algorithmus
Aus Video: https://www.youtube.com/watch?v=X3B-24de5Oo (Quelle)
Kostenmaß: print-Funktion (da Eingabe/Ausgabe idR. langsam)
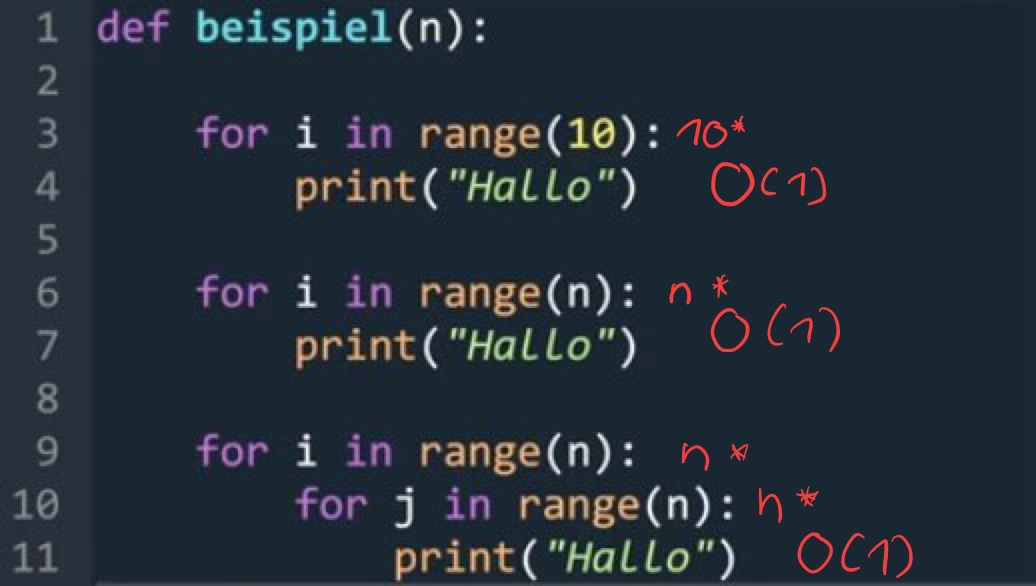
n² + n + 10 ∈ O(n²)
¶ Selection Sort
Hausaufgabe: Versuchen Sie anhand des Codes die Komplexitätsklasse von SelectionSort zu bestimmen
Kostenmaß: Vergleiche (siehe Zeile 8)
# Selection Sort
def selection_sort(liste):
# Für nächstes noch nicht sortiertes Element
for index_unsortiert in range(len(liste)):
# Finde Index des kleinsten Elements
index_min = index_unsortiert
for index_next in range(index_unsortiert + 1, len(liste)):
if liste[index_next] < liste[index_min]:
index_min = index_next
# Tausche
liste[index_min], liste[index_unsortiert] = liste[index_unsortiert], liste[index_min]
return liste
- Schleife in Zeile 4 wiederholt sich n mal
- Schleife in Zeile 7 wiederholt sich unterschiedlich häufig. Je Aufruf folgende Anzahl an Vergleichen:
n-1
n-2
n-3
....
3
2
1
Mit dem kleinen Gauß (Gauß-Summe) lässt sich die Summe dieser Zahlen berechnen und nach den Regeln von oben vereinfachen.